Introduction
Dans le dernier rapport du GIEC, il est noté que la température moyenne mondiale a augmenté de 1,1 °C depuis l’ère préindustrielle et le seuil de 1,5 °C pourrait être franchi d’ici 2040. Cette hausse devrait se poursuivre jusqu’à la moitié du siècle à minima. En fin de siècle, elle se situerait entre 1,4 °C [1-1,8] à 4,4 °C [3,3-5,7] selon les différentes trajectoires climatiques. Le changement climatique se traduit aussi par une modification du cycle de l’eau et s’il y a une plus forte incertitude sur l’évolution des cumuls de précipitations annuelles, il apparaît que les événements hydriques extrêmes comme les fortes pluies et les sécheresses (photo 1) sont plus fréquents (IPCC, 2021).
Photo 1 - Vue sur la Loire et sur l'Île Sorin à La Bohalle (49) en période de sécheresse
Crédit photo : Cramos (commons.wikimedia.org), CC BY-SA 4.0 Deed, 2018
Concernant l’évolution des précipitations annuelles, il n’y a pas de tendance homogène tant à l’échelle mondiale (IPCC, 2021) ou française (Jouzel et al., 2014) qu’au niveau régional (Merot et al., 2012 ; Comité 21 Grand Ouest, 2022 ; Amiot et al., 2023).
En Pays de la Loire, le rapport du GIEC régional indique que les risques climatiques (sécheresses, vagues de chaleur, fortes pluies) sont et seront généralement plus fréquents et intenses à l’avenir avec par exemple, 10 à 30 jours chauds en plus (jours ou les températures maximales excèdent 25 °C) en fin de siècle et « une baisse sensible des ressources en eau souterraines de la région » (Comité 21 Grand Ouest, 2022).
La connaissance du climat au niveau régional et local est donc un des enjeux actuels majeurs pour les collectivités territoriales notamment en vue d’établir des politiques d’adaptation au changement climatique. Or, les données ne sont disponibles que ponctuellement ou nationalement ce qui ne permet pas de montrer les subtilités d’un climat local et les variations spatiales infrarégionales.
L’objectif de ce travail est de contribuer au développement des connaissances sur le changement climatique régional en spatialisant les données régionales afin de disposer d’un rendu cartographique à une échelle de 1 km sur les Pays de la Loire pour le climat actuel et futur. Ce travail complète et actualise l’Atlas climatologique régional réalisé en 2013 : celui-ci avait une résolution de 5 km et avait été effectué avec les scénarios SRES du 4e rapport du GIEC (Météo France, 2013). Ce travail a été réalisé dans le cadre des programmes FERMADAPT et CLIMAVEG qui visent à étudier les impacts du changement climatique sur l’agriculture dans la région.
Données et méthodes
La spatialisation régionale du changement climatique fait usage de données de nature différente, climatique et géographique.
Sélection des données climatiques
Afin d’obtenir la meilleure représentativité climatique du territoire, il est nécessaire de sélectionner un nombre suffisant de séries de données stationnelles. Celles-ci sont sélectionnées selon des critères de qualité : la série de données doit être suffisamment longue, sans interruption et statistiquement homogène comme précisé dans le rapport de l’OMM (2013). Ainsi, les données prises en compte correspondent aux séries mensuelles homogénéisées par Météo-France, dont la méthode est précisée dans l’étude de Moisselin et al. (2002). Les séries démarrent majoritairement autour de 1951, ce qui permet de comparer deux normales climatiques de 30 ans, sur la période observée : 1951-1980 et 1991-2020.
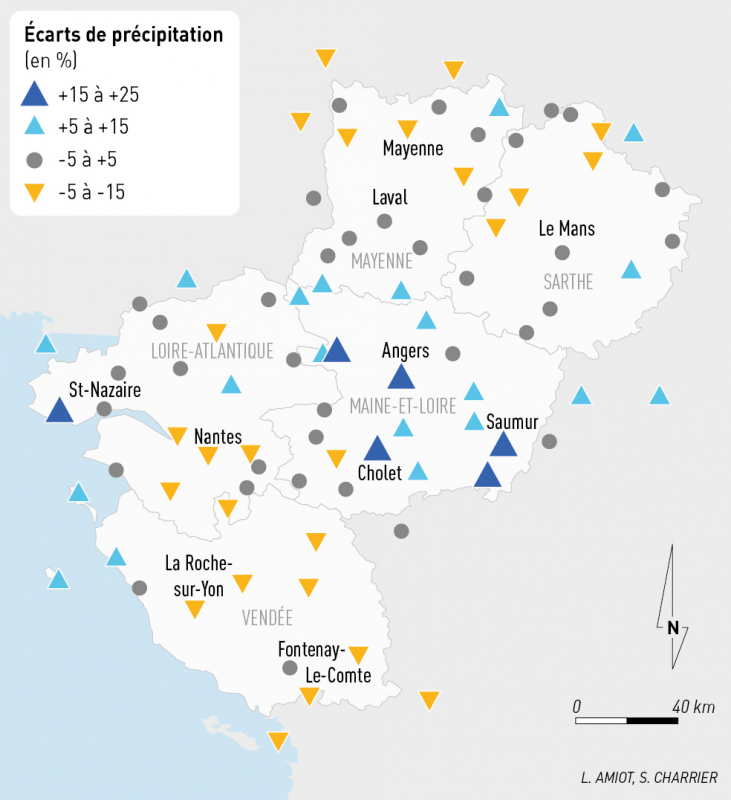
Au total, 91 séries de données de précipitations, dont 28 de températures, sont prises en compte pour la cartographie du changement climatique. Parmi celles-ci, 16 séries de données de précipitations et 4 pour les températures sont situées en dehors de la limite administrative régionale (fig. 1). Cela donne une meilleure représentativité du climat régional, notamment proche des limites de la région.
La répartition spatiale des séries de données est assez homogène sur l’ensemble de la région avec au moins quatre stations de température et douze stations de précipitations par département (fig. 1). Pour les données de température, il y a une surreprésentation des stations littorales avec près de 25 % situées à moins de 10 km de la mer alors que cela ne représente en réalité que 7 % de la surface de la région. On note aussi une surreprésentation des stations situées à l’ouest (longitude entre -2 et-2,5°) avec 20 % des stations contre une surface réelle couvrant moins de 5 % de la superficie régionale. La répartition latitudinale et altitudinale des séries de données est davantage régulière. Pour les précipitations, le réseau montre une très bonne répartition géographique des stations.
L’étude des températures s’effectue d’abord au niveau annuel pour avoir les tendances générales. Puis, pour visualiser l’ampleur du changement le choix a été fait de cartographier le mois le plus froid (janvier) et le mois le plus chaud (juillet).
L’étude de la pluviométrie s’effectue à l'échelle annuelle et par saison hydrologique. Les précipitations sont étroitement liées au cycle de l’eau, dont l’hydrologie des cours d’eau, mais aussi au cycle végétal. Ainsi deux saisons hydrologiques se distinguent :
la saison de recharge (octobre à mars) des nappes et des cours d’eau correspond à la période la plus arrosée de l’année, avec une végétation en dormance. Les précipitations viennent recharger les réserves en eau de surface ou s’infiltrent dans le sol. Une infime partie s’évapore du fait de températures modérées/basses ;
la saison d’étiage (avril à septembre) est la saison où les pluies sont généralement moins présentes et la végétation est en pleine activité avec un besoin en eau accru. Les précipitations durant cette période sont majoritairement absorbées par la végétation et les cours d’eau ont tendance à s’assécher.
Les données climatiques futures
Les données climatiques futures dépendent de différents modèles et scénarios d’évolution du climat. Celles-ci sont extraites à partir du portail Drias1, avec les dernières actualisations des scénarios Representative Concentration Pathway (RCP) du 5e rapport du GIEC (IPCC, 2013) présentées par Soubeyroux et al. (2020). Le modèle pris en compte est le CNRM-CM5/Aladin63 (nommé CNRM par la suite dans le texte), fréquemment utilisé pour étudier l’évolution climatique en France (Jouzel et al., 2014 ; Dubreuil et al., 2022). Il est considéré comme un modèle médian parmi l’ensemble des modèles disponibles sur le portail Drias (Soubeyroux et al., 2020).
Les scénarios RCP prennent en compte l’évolution des concentrations de gaz à effet de serre dont les trajectoires sont définies dans l’étude de R. Moss et al. (2010). Ici, les scénarios RCP 4.5 et RCP 8.5 sont utilisés. Le scénario RCP 4.5 correspond à un scénario intermédiaire avec une stabilisation des émissions de gaz à effet de serre d’ici 2030 puis baisse à partir de 2050 et le scénario RCP 8.5 correspond à un scénario d’évolution des concentrations en gaz à effet de serre pessimiste avec une hausse continue des émissions. Pour chacune des 91 stations, la donnée future modélisée est considérée comme étant celle du point de la grille SAFRAN, présentée par J-M. Soubeyroux et al. (2008), la plus proche.
Figure 2 - Répartition des écarts entre les données observées et les données du modèle CNRM sur la période 1976-2005 pour les 28 séries de données de température (A) et 91 séries de précipitation (B)
Les données passées modélisées sur la période de référence de Drias (1976-2005) ont été confrontées aux données observées sur la même période pour vérifier les écarts entre les données modélisées et observées station par station.
Pour les températures moyennes, les écarts sont effectivement quasiment négligeables à l'échelle annuelle, la médiane étant proche de 0. Cependant, le biais annuel peut tout de même dépasser 0,4 °C pour quelques stations. Pour les mois de janvier et juillet, le biais est plus fort avec une sous-estimation médiane de 0,3 °C en janvier et une surestimation médiane de 0,2 °C en juillet dépassant ponctuellement 0,5 °C (fig. 2A).
Les biais de précipitations sont plus hétérogènes, le biais annuel médian est de -2 % environ mais il peut atteindre -15 % à +10 %. Le cumul de précipitation est davantage sous-estimé par le modèle CNRM durant la saison de recharge et généralement légèrement surestimé en saison d’étiage (fig. 2B).
Les biais n’étant finalement pas négligeables, le choix a donc été fait de corriger les données futures issues de Drias. La correction du biais s’effectue par une soustraction des biais préalablement calculée entre les données observées et les données modélisées sur la période historique et sur la période de référence Drias (1976-2005) aux données modélisées futures comme c’est le cas dans l’ouvrage de P. Merot et al. (2012), ou encore dans les thèses de C. Lamy (2013) et F. Beauvais (2021) :
𝒙𝒄𝒐𝒓𝒓 = 𝒙𝒎𝒐𝒅 - ∆𝑟𝑒𝑓𝟏𝟗𝟕𝟔-𝟐𝟎𝟎𝟓
Avec :
𝒙𝒄𝒐𝒓𝒓= donnée modélisée corrigée
𝒙𝒎𝒐𝒅 = donnée modélisée brute
∆𝑟𝑒𝑓𝟏𝟗𝟕𝟔-𝟐𝟎𝟎𝟓 = écart entre la donnée modélisée et la donnée observée sur la période de référence drias (1976-2005).
Une fois cette correction effectuée, la méthode de régionalisation est appliquée aux données futures.
Méthode de régionalisation des données
D’après R. Caloz et C. Collet (2011), la régionalisation consiste à affecter une propriété statistique qui décrit un ensemble de points à tout point d’un espace considéré à partir d’un nombre suffisant de données pour assurer une représentativité spatiale du phénomène.
Pour régionaliser les températures ou les précipitations, il existe plusieurs méthodes dites d’interpolation qui permettent de restituer un ensemble de valeurs sur une surface donnée à partir de mesures ponctuelles. Le but est de prédire la valeur théorique sur l’ensemble d’un territoire à partir d’un réseau de mesures (Siu-Ngang Lam, 1983). D’après D. Joly et al. (2008), il existe trois grandes familles de méthodes d’interpolation : le krigeage, la régression et une méthode mixte régression-krigeage. Ces méthodes sont applicables en géographie sous le nom de géostatistique lorsque les variables prises en compte sont des variables géographiques telles que la latitude ou l’altitude.
Les méthodes d’interpolations purement spatiales comme le krigeage n’offrent pas toujours de résultats satisfaisants en climatologie parce qu’elles ne prennent pas en compte la variabilité des paramètres géographiques, mais dépendent de la distance entre chaque point. L’approche la plus commune consiste donc à prendre en compte les autres variables qui influencent directement les températures et les précipitations comme l'a montré R. Lhotellier (2006).
Pour régionaliser les données, le choix a été fait ici d’utiliser la méthode de régression multiple. Elle est définie par M. Arnaud et X. Emery (2000) comme étant une méthode d’interpolation déterministe qui consiste à estimer la valeur d’une variable en tout point d’un territoire donné.
La relation d’une régression multiple correspond ici à une relation linéaire entre une variable recherchée et des variables mesurées. Chaque coefficient est calculé de manière à réduire au maximum l’écart entre le point mesuré et la courbe de tendance suivant la méthode des moindres carrés (Caloz et Collet, 2011).
Sa formule se définit ainsi : 𝑍= 𝑎0+ 𝑎1× 𝑥 + 𝑎2× 𝑦 + ⋯
Avec 𝑍, la variable dépendante et 𝑥, 𝑦, etc., les variables explicatives. Cette méthode permet de définir la distribution spatiale d’un phénomène sur le territoire. Les données géographiques et environnementales interviennent dans la modélisation comme variables explicatives (Arnaud et Emery, 2000). Les cartes climatiques détaillées de la France présentées par A. Douguedroit et M-F. De Saintignon (1970) sont un exemple emblématique d’une première tentative de spatialisation du climat par interpolation d’une régression entre température et altitude. Cette méthode est couramment utilisée pour spatialiser le climat à échelle fine (Peguy et al., 1984 ; Carrega, 2003 ; Joly et al., 2010 ; Bonnefoy et al., 2014 ; Fortin et Dubreuil, 2020 ; Amiot et al., 2023).
Les variables géographiques prises en compte ici sont : la latitude, la longitude, la distance à la mer, l’altitude. Les variables d’occupation du sol utilisées dans certaines études comme celle de D. Joly et al. (2008) ou V. Dubreuil et al. (2002) ne sont pas prises en compte pour ne pas ajouter à l’incertitude de l’évolution climatique, l’incertitude de l’évolution de l’occupation du sol.
Une base de données avec les références spatiales et les paramètres géographiques pour chacun des points du territoire a été extraite du Modèle Numérique de Terrain (MNT) SRTM2 qui a une résolution spatiale de 90 mètres.
Avec les variables énoncées précédemment, la régression multiple revient à calculer pour un point donné :
𝐷𝑥= 𝑎0+ 𝑎1× 𝑎𝑙𝑡𝑥 + 𝑎2× 𝑙𝑎𝑡𝑥+ 𝑎3× 𝑙𝑜𝑛𝑔𝑥+ 𝑎4× 𝑑𝑖𝑠𝑡𝑥
Avec D𝑥 la donnée climatique (température ou précipitation) estimée du point 𝑥 considéré, alt l’altitude en mètre, lat la latitude, long la longitude et dist la distance à la mer.
Avec ces quatre variables, il est possible d’obtenir un résultat significatif pour l’ensemble des points à 1 km de résolution. Les coefficients varient selon la donnée climatique recherchée, ils sont ajustés par la méthode des moindres carrés.
Afin de tester l’efficacité du modèle de régionalisation, les données climatiques modélisées ont été comparées aux données climatiques observées sur la période 1991-2020.
Résultats
Les températures
Les résultats statistiques du modèle de régionalisation pour les températures annuelles
Le modèle de régionalisation a été appliqué pour les températures. Ce modèle présente de forts coefficients de corrélation pour l’ensemble des périodes étudiées (autour de 0,9 ; tab. 1). Les variables ayant le plus de poids sont la latitude et l’altitude avec des coefficients standardisés respectivement autour de -0,4 et -0,5 (tab. 2). Par exemple, il y a une perte de 0,3 °C pour une élévation de 100 m sur la température annuelle sur l’ensemble des périodes et une perte de 0,4 °C pour un déplacement de 1° Nord (tab. 1).
Tableau 1 - Résultats de la régression multiple pour les températures moyennes annuelles
| Altitude | Longitude | Latitude | Distance à la mer | Constante | Coeff. de corrélation | ||
| OBS | 1951-1980 | -0,003 | -0,2 | -0,37 | 0 | 28,7 | 0,86 |
| 1991-2020 | -0,003 | -0,18 | -0,57 | 0,001 | 39,45 | 0,92 | |
| RCP 4.5 | 2031-2060 | -0,003 | -0,22 | -0,52 | 0,002 | 37,8 | 0,9 |
| 2071-2100 | -0,003 | -0,21 | -0,49 | 0,002 | 37,1 | 0,89 | |
| RCP 8.5 | 2031-2060 | -0,003 | -0,25 | -0,52 | 0,002 | 37,92 | 0,9 |
| 2071-2100 | -0,003 | -0,23 | -0,55 | 0,003 | 41,2 | 0,89 |
Tableau 2 - Coefficients de régression standardisés des différentes variables explicatives des températures moyennes annuelles sur différentes périodes
| Altitude | Longitude | Latitude | Distance à la mer | ||
| OBS | 1951-1980 | -0,4 | -0,28 | -0,4 | 0,03 |
| 1991-2020 | -0,35 | -0,26 | -0,61 | 0,12 | |
| RCP 4.5 | 2031-2060 | -0,37 | -0,31 | -0,56 | 0,17 |
| 2071-2100 | -0,39 | -0,3 | -0,54 | 0,17 | |
| RCP 8.5 | 2031-2060 | -0,37 | -0,34 | -0,55 | 0,19 |
| 2071-2100 | -0,39 | -0,31 | -0,54 | 0,17 |
Il apparaît que les biais de régionalisation restent inférieurs à 0,5 °C pour la température moyenne annuelle. Les données des stations littorales sont légèrement sous-estimées, pour le reste il n’y a pas de logique géographique concernant ces biais (fig. 3).
Figure 3 - Écarts entre les données régionalisées et les données observées en moyenne sur la période 1991-2020 pour les températures moyennes annuelles
L’évolution des températures moyennes annuelles
La régionalisation à un kilomètre permet de rendre compte de la répartition et de l’ampleur du changement des températures dans la région. En Pays de la Loire, il existe un gradient altitudinal avec un écart de 1 à 2 °C entre les collines du Maine par rapport à la vallée de la Loire. Ensuite, le gradient latitudinal s’observe avec un écart de l’ordre de 2 °C en moyenne à l’année entre l’extrême Sud vendéen et le Nord Pays de la Loire. Il y a aussi un effet longitudinal lié notamment à la distance à la mer avec une température qui diminue en s’éloignant de la côte. Cet effet est particulièrement visible en Loire-Atlantique et en Vendée (fig. 3).
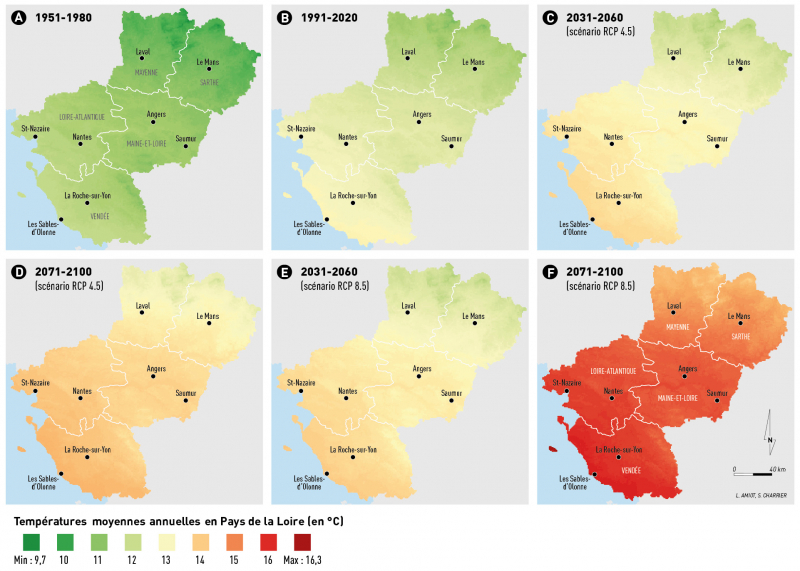
Une augmentation de 1 à 1,5 °C de la température moyenne annuelle s’est produite entre la période 1951-1980 et 1991-2020. En effet, alors que près d’un tiers nord de la région a une température moyenne annuelle inférieure à 11 °C sur la période 1951-1980, la température moyenne annuelle dépasse quasiment les 11°C dans toute la région sur la période 1991-2020 (fig. 4A et 4B). Les températures sont situées entre 11 °C au nord de la région et 13 °C au Sud sur cette période 1991-2020.
Figure 4 - Températures moyennes annuelles en Pays de la Loire pour les périodes 1951-1980 (A), 1991-2020(B), puis les périodes futures 2031-2060 (C) et 2071-2100 (D) pour le scénario RCP 4.5 et 2031-2060 (E) et 2071-2100 (F) pour le scénario RCP 8.5 issues du modèle CNRM
À horizon moyen (période 2031-2060), la température moyenne annuelle devrait continuer à progresser dans le même sens et au même rythme que celui observé indépendamment du scénario d’évolution climatique considéré. Sur cette période, environ 70 % du territoire connaîtrait des températures supérieures à 13 °C, contre 10 % situé principalement sur le littoral vendéen sur la période 1991-2020 (fig. 4B, 4C et 4E).
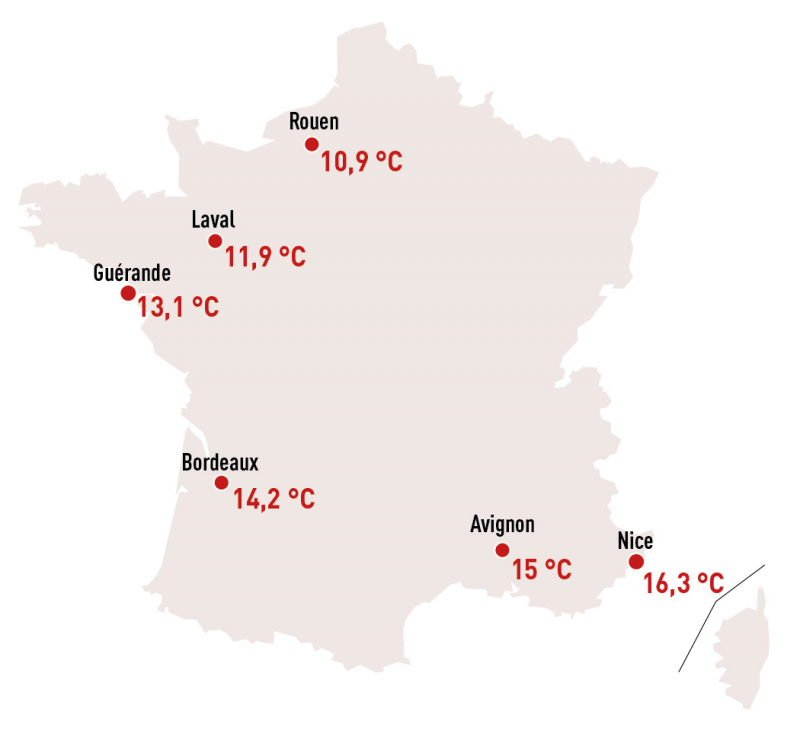
À horizon lointain, la hausse se poursuit sur un rythme qui dépend du scénario. Dans le scénario RCP 4.5, celle-ci est de +1,3 °C, avec des températures moyennes annuelles qui atteignent 12,5 à 14,5 °C (fig. 4D). Les températures moyennes annuelles de Vendée et de Loire-Atlantique correspondraient à celles observées sur la période 1991-2020 autour de Bordeaux (fig. 5). Dans le RCP 8.5, la hausse est située autour de 3 °C. Les températures moyennes annuelles atteignent donc 14 à 16 °C, les températures moyennes annuelles du Sud de la Vendée s’approchent de celles de Nice sur la période 1991-2020 (fig. 4F, fig. 5). Seulement 15 % du territoire, au nord d’un axe Laval - Le Mans aurait ici une température moyenne annuelle inférieure à 15 °C, l’équivalent de la normale climatique d’Avignon sur la période 1991-2020 (fig. 4F, fig. 5).
L’évolution des températures saisonnières
Les résultats statistiques du modèle de régionalisation pour les températures de janvier et juillet
L’évolution de la température pouvant être observée à toute saison, nous avons fait le choix, comme précédemment pour les températures, de cartographier le mois le plus froid (janvier) et le mois le plus chaud (juillet).
Le modèle de régionalisation a été appliqué pour les températures moyennes de janvier et juillet sur les mêmes périodes que les températures annuelles afin de cartographier l’évolution des températures sur ces deux mois. Concernant les régressions, il y a une forte corrélation pour l’ensemble des données calculées, autour de 0,9. Un changement de signe s’observe concernant le coefficient de la longitude : négatif en janvier, soit une perte de température pour un déplacement vers l’Est, et positif en juillet (tab. 3). Ce changement de signe s’observe aussi pour les régressions standardisées. La longitude est d’ailleurs un paramètre contribuant fortement à la régionalisation des données du mois de janvier avec une régression autour de -0,5 à -0,7. En juillet, c’est la latitude et l’altitude avec un coefficient standard autour de -0,7 (tab. 4).
Tableau 3 - Résultats statistiques issus de la régression multiple pour les données de température en janvier et juillet
| Altitude | Longitude | Latitude | Distance à la mer | Constante | Coeff. de corrélation | ||
| JANVIER | 1951-1980 | -0,003 | -0,7 | -0,33 | 0 | 19,53 | 0,93 |
| 1991-2020 | -0,003 | -0,55 | -0,35 | 0 | 22,3 | 0,95 | |
| 2071-2100 RCP4.5 | -0,003 | -0,57 | -0,3 | 0 | 20,36 | 0,95 | |
| 2071-2100 RCP8.5 | -0,003 | -0,49 | -0,35 | 0 | 24,91 | 0,94 | |
| JUILLET | 1951-1980 | -0,004 | 0,1 | -0,53 | 0 | 43,36 | 0,77 |
| 1991-2020 | -0,004 | 0,1 | -0,53 | 0 | 43,36 | 0,91 | |
| 2071-2100 RCP4.5 | -0,004 | 0,04 | -0,7 | 0,01 | 53,9 | 0,89 | |
| 2071-2100 RCP8.5 | -0,004 | 0,2 | -0,75 | 0,01 | 58,76 | 0,9 |
Tableau 4 - Coefficient de régression standardisé des différentes variables pour les données
| Altitude | Longitude | Latitude | Distance à la mer | ||
| JANVIER | 1951-1980 | -0,22 | -0,71 | -0,25 | 0,06 |
| 1991-2020 | -0,292 | -0,59 | -0,31 | 0,02 | |
| 2071-2100 RCP4.5 | -0,29 | -0,64 | -0,26 | 0,04 | |
| 2071-2100 RCP8.5 | -0,36 | -0,59 | -0,32 | 0,03 | |
| JUILLET | 1951-1980 | -0,45 | 0,14 | -0,56 | 0,32 |
| 1991-2020 | -0,412 | 0,38 | -0,74 | 0,31 | |
| 2071-2100 RCP4.5 | -0,427 | 0,05 | -0,72 | 0,5 | |
| 2071-2100 RCP8.5 | -0,364 | 0,24 | -0,7 | 0,59 |
Évolution des températures en janvier et juillet
La température de janvier a augmenté de près de 1,5 °C en moyenne sur la région entre la période 1951-1980 et 1991-2020. Cela se traduit spatialement par une augmentation de la superficie ou la température dépasse 5 °C : cela concernait 30 % sur la normale 1951-1980 de la surface régionale contre 89 % sur 1991-2020 (fig. 6A et 6B). En fin de siècle, la température de janvier augmente à des degrés différents selon le scénario : dans le cas du scénario RCP 4.5, la hausse est de l’ordre de 1 °C par rapport à la normale climatique 1991-2020 avec un décalage toujours plus à l’Est de la douceur hivernale caractéristique du climat océanique. La température moyenne hivernale sera supérieure à 5 °C sur toute la région dans ce scénario (fig. 6C). Avec le RCP 8.5, la hausse de la température est plus forte avec près de 3 °C supplémentaires par rapport à la normale climatique 1991-2020. Ici, la température est supérieure à 8 °C sur toute la région avec un gradient thermique est-ouest réduit (fig. 6D).
Figure 6 - Températures moyennes en janvier sur la période observée 1951-1980 (A), 1991-2020 (B), et la période future 2071-2100 d’après les scénarios RCP 4.5 (C) et RCP 8.5 (D)
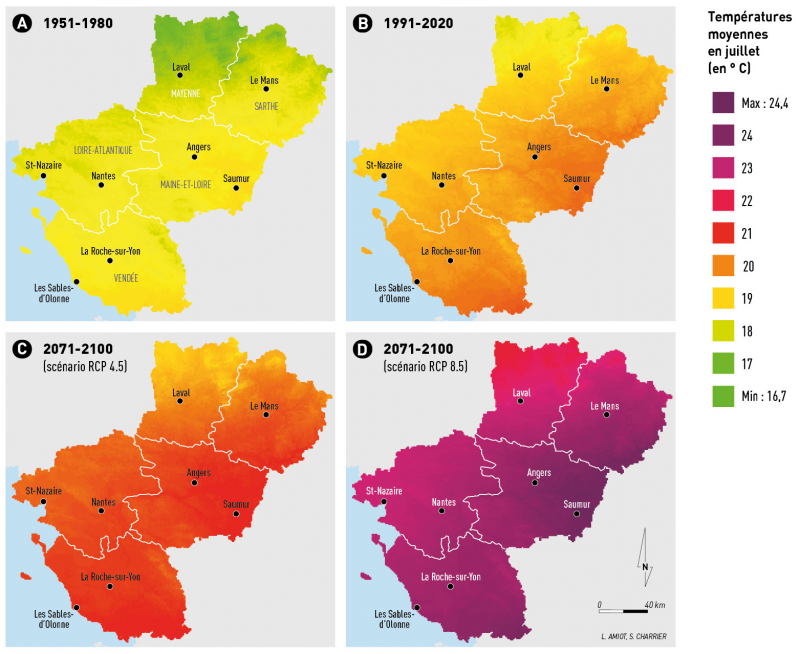
En juillet, la température moyenne est de l’ordre de 18,5 à 20 °C sur la période 1991-2020 avec un net gradient thermique nord-sud entre le nord de la Mayenne et le sud de la Vendée. La hausse de température déjà observée est de l’ordre de 1 °C à plus de 1,5 °C par rapport aux données de 1951-1980. Ainsi, seulement 10 % du territoire (situé en nord Mayenne) connait des températures moyennes en juillet inférieures à 19 °C sur 1991-2020 contre 99 % du territoire pour la période 1951-1980 (fig. 7A et 7B). À horizon lointain, la hausse est variable selon le scénario : elle est limitée à 1 °C pour le scénario RCP 4.5 avec une température moyenne qui dépasserait 20 °C sur l’ensemble du territoire, dont 80 % de la surface avec une température située entre 21 et 22 °C (fig. 7C). Dans le scénario RCP 8.5, la hausse de la température est de +3 à +4 °C par rapport à 1991-2020. La température moyenne estivale dépasse ici 22 °C sur la quasi-totalité du territoire excepté le nord de la Mayenne, tandis que la région de Saumur connaîtrait une température moyenne supérieure à 24 °C, soit l’équivalent du mois de juillet 20223 ou encore la température moyenne de juillet à Montpellier4 sur la période 1991-2020 (fig. 7D).
Figure 7 - Températures moyennes en juillet sur la période observée 1951-1980 (A), 1991-2020 (B), et la période future 2071-2100 d’après les scénarios RCP 4.5 (C) et RCP 8.5 (D)
La pluviométrie
Les résultats statistiques du modèle de régionalisation pour les données de précipitations annuelles et saisonnières
Les données de précipitation ont été cartographiées suivant la même méthode et les mêmes paramètres géographiques. Les coefficients de corrélation sont inférieurs aux températures, ils sont situés autour de 0,7 (tab. 5). La distance à la mer est un paramètre qui contribue fortement dans la relation régression avec une relation négative qui donne une diminution des précipitations annuelles et saisonnières avec l’éloignement à la mer (tab. 6). Celle-ci est par exemple de -136 à -177 mm pour un éloignement de 100 km de la mer.
Tableau 5 - Résultats statistiques issus de la régression multiple pour les données de précipitations annuelles et par saison hydrologique
| Altitude | Longitude | Latitude | Distance à la mer | Constante | Coeff. de corrélation | ||
| ANNUEL | 1951-1980 | 0,698 | 41,8 | 16,0 | -1,8 | 95,18 | 0,74 |
| 1991-2020 | 0,499 | 8,4 | 17,9 | -1,4 | 5,93 | 0,66 | |
| RECHARGE | 1951-1980 | 0,447 | 15,5 | 1,2 | -1,1 | 430,34 | 0,76 |
| 1991-2020 | 0,343 | -8,6 | -2,0 | -0,9 | 576,37 | 0,72 | |
| ETIAGE | 1951-1980 | 0,236 | 25,9 | 14,6 | -0,6 | -332,87 | 0,74 |
| 1991-2020 | 0,167 | 18,6 | 18,5 | -0,5 | -513,65 | 0,68 |
Tableau 6 - Coefficient de régression standardisé des différentes variables pour les données de précipitation
| Altitude | Longitude | Latitude | Distance à la mer | ||
| ANNUEL | 1951-1980 | 0,47 | 0,38 | 0,11 | -0,95 |
| 1991-2020 | 0,35 | 0,08 | 0,13 | -0,76 | |
| RECHARGE | 1951-1980 | 0,47 | 0,22 | 0,01 | -0,94 |
| 1991-2020 | 0,34 | -0,12 | -0,02 | -0,68 | |
| ETIAGE | 1951-1980 | 0,42 | 0,63 | 0,26 | -0,86 |
| 1991-2020 | 0,32 | 0,49 | 0,36 | -0,74 |
Pour les précipitations, les écarts sont plus hétérogènes avec une sous-estimation du cumul de précipitations au nord de la Loire-Atlantique et en Vendée allant jusqu’à -15 % du cumul annuel. À l’inverse, le littoral et le Saumurois ont ici une forte surestimation de leur cumul annuel moyen. Le reste des stations ont des biais limités (fig. 8).
Figure 8 - Écarts entre les données régionalisées et les données observées en moyenne sur la période 1976-2005 pour les précipitations annuelles
La pluviométrie et son évolution en Pays de la Loire
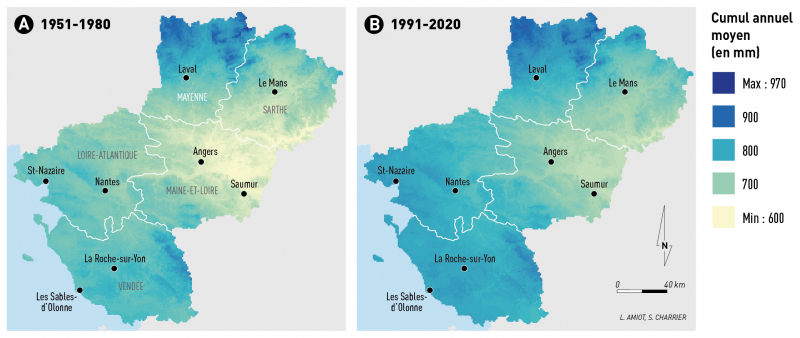
Il y a une différence spatiale concernant la répartition des cumuls pluviométriques annuels et saisonniers. En se fondant sur la période 1991-2020, la région peut être découpée en trois ensembles : le littoral qui est généralement bien arrosé (autour de 800 mm) avec un fort contraste pluviométrique entre saison d’étiage et saison de recharge, plus de 60 % du cumul annuel s’effectue durant la saison de recharge ; le centre de la région entre Angers, Saumur et Le Mans est moins arrosé (entre 600 et 700 mm annuel), mais le contraste saisonnier est réduit ; et le nord-ouest de la région, principalement la Mayenne qui est bien arrosée (autour de 900 mm à l’année) avec un contraste saisonnier peu marqué (fig 9B ; 10C ; 10D). Cette répartition spatiale n’a pas évolué sur la période observée car l’augmentation du cumul est assez uniforme sur la région et concerne les deux saisons hydrologiques.
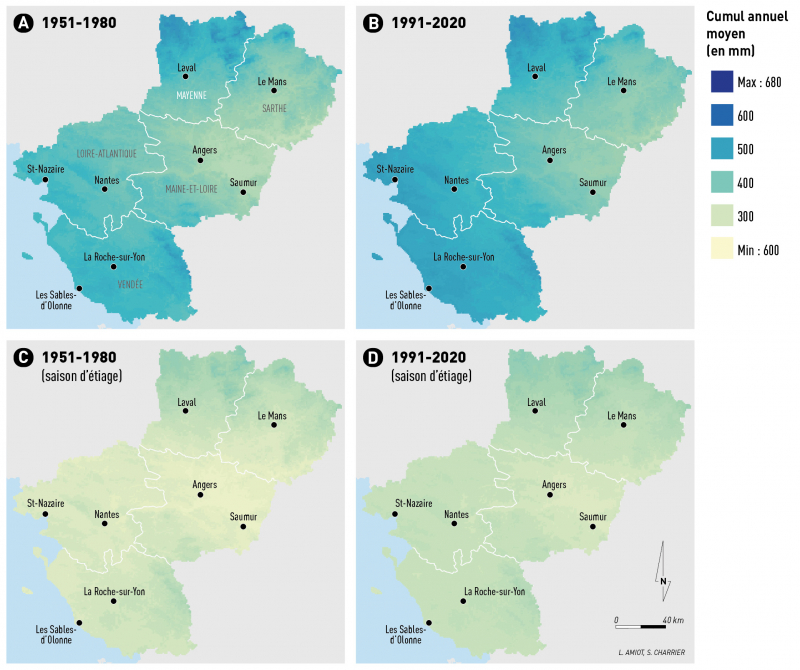
Figure 10 - Cumul de précipitations par saison hydrologique, en saison de recharge sur les périodes observées 1951-1980 (A), 1991-2020 (B), et en saison d’étiage sur les périodes observées 1951-1980 (C), 1991-2020 (D)
Le cumul pluviométrique annuel a augmenté en moyenne de 7 % soit en moyenne +45 mm sur l’année entre les périodes 1991-2020 et 1951-1980, ce qui est l’équivalent d’un mois de pluie d’été en plus (fig. 9A ; 9B).
La hausse du cumul peut s’observer sur les deux saisons hydrologiques avec en saison de recharge un cumul de près de 400 mm sur une large partie ouest du territoire aujourd’hui alors que cela ne concernait que les collines du Maine et vendéennes en 1951-1980 (fig. 10A ; 10B) et en saison d’étiage plus de 300 mm sur toute la région exceptée un axe Angers-Saumur alors que cette zone occupait la Loire Atlantique et le Maine-et-Loire en 1951-1980 (fig. 10C et 10D).
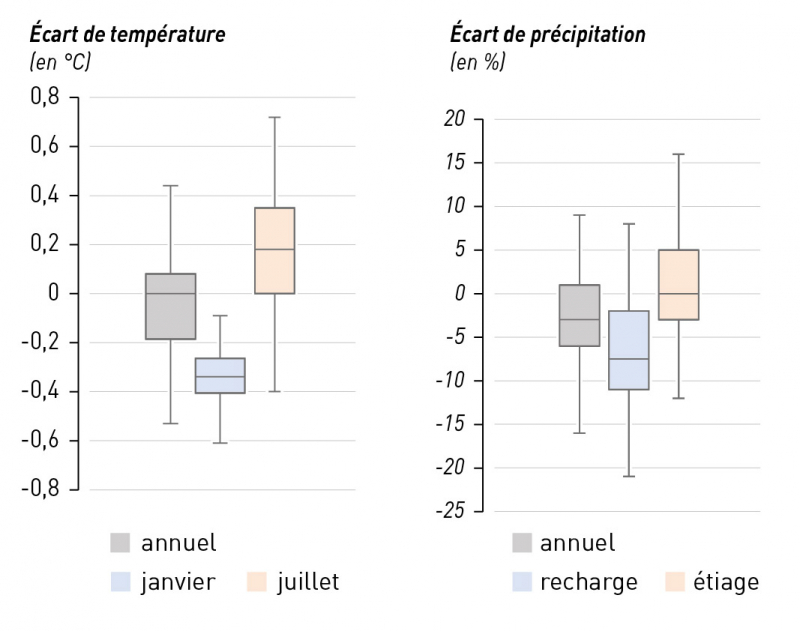
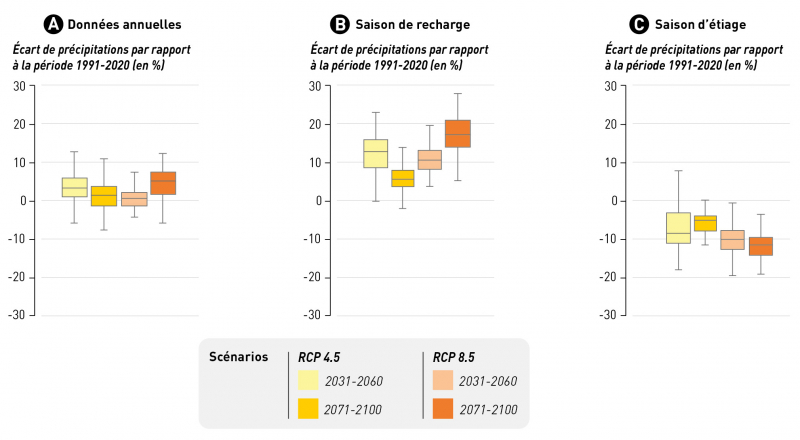
L’évolution future des précipitations annuelles tend vers une légère augmentation qui reste en moyenne inférieure à 5 % dans tous les cas (fig.11A).
Figure 11 - Répartition des écarts de précipitations sur l’ensemble des stations de la région Pays de Loire entre la période observée 1991-2020 et les périodes futures modélisées sous conditions RCP 4.5 et RCP 8.5 (modèle CNRM) pour les données annuelles (A), en saison de recharge (B) et saison d’étiage (C)
Si le cumul reste relativement stable à horizon moyen comme à horizon lointain, une amplification du contraste pluviométrique saisonnier est projetée par le modèle. En effet, le cumul de précipitation tend à augmenter en saison de recharge et baisser en saison d’étiage. La hausse en saison de recharge est de l’ordre de 10 % à horizon moyen et 6 à 17 % à horizon lointain, la hausse étant plus forte dans le scénario RCP 8.5 (fig. 11B). En saison d’étiage, la baisse du cumul est de l’ordre de 10 % avec une baisse plus importante dans le scénario RCP 8.5 (fig. 11C).
Discussion et conclusion
L’approche cartographique apporte des biais dus à la méthode de régionalisation des données. Des résidus de modèle géostatistique persistent, car les paramètres géographiques ne sont pas les seuls à influencer le climat (Lhotellier, 2006). Les résidus restent tout de même assez limités ici, particulièrement pour les températures.
L’usage du seul modèle climatique CNRM-ALADIN conduit à nuancer la vision de l’évolution climatique. Il est identifié par Soubeyroux et al. (2020) comme étant parmi les 3 modèles du portail drias5 qui simule un réchauffement moins important en hiver et une évolution des précipitations hivernales situées dans la médiane pour l’ensemble des scénarios en fin de siècle. L’usage de ce seul modèle occulte la vision d’un modèle qui réchaufferait plus ou moins selon la saison. Même si les tendances sont convergentes pour les températures, il serait intéressant d’étudier l’évolution d’après un modèle plus ou moins réchauffant et plus ou moins humidifiant.
Par ailleurs, les nouveaux scénarios SSP du 6e rapport du GIEC pourront donner une idée plus précise de l’évolution climatique en France. D’après Ribes et al. (2022), il est possible que ceux-ci présentent un réchauffement climatique plus prononcé en France. Cependant, les données ne sont à ce jour pas disponibles à une échelle de 8 km sur le portail Drias.
Si le climat des Pays de Loire se réchauffe plus ou moins rapidement selon les scénarios, la répartition spatiale relative des températures et des précipitations n’est pas modifiée par le changement climatique : les territoires régionaux les plus chauds (littoral vendéen notamment) resteront les mêmes avec une température plus élevée de 1 à 3 °C par rapport à la période 1991-2020. Cela correspond à un décalage des isothermes de 1 à 3° de latitude vers le nord (110 à 330 km) en fin de siècle, déjà observable depuis 1951. Des observations similaires sont relevées en Bretagne (Amiot et al., 2023).
Le réchauffement s’observe en été comme en hiver, avec des températures moyennes qui pourront dépasser 22 °C en juillet en moyenne, mais aussi en août dans le scénario RCP 8.5 sur la période 2071-2100, seuil utilisé notamment pour définir des étés chauds en milieu tempéré dans la classification des climats de Köppen (Koppen, 1900). La baisse concomitante des précipitations sur la période d’étiage comprenant la période estivale rendrait les étés de la région comparables à ceux de la France méditerranéenne actuelle. Cette évolution du climat vers des étés chauds et secs peut être qualifiée comme une méditerranisation du climat (Dubreuil, 2022).
En hiver, le contraste thermique entre l’Est et l’Ouest de la région se réduit, les températures moyennes de janvier pourraient dépasser 7 °C en fin de siècle dans le RCP 8.5. Le réchauffement hivernal pourrait par exemple causer des problèmes pour les productions arboricoles qui ont un certain besoin en froid (Berthoumieu et al., 2022). Cet adoucissement hivernal pose aussi une question de santé publique avec une facilitation de la survie des virus (Marano et Toussaint, 2015).
La partie est de la région située entre Le Mans, Angers et Saumur semble être la plus sensible au niveau de l’évolution climatique. En effet, avec des étés de plus en plus chauds et un cumul de précipitation sur la saison d’étiage (incluant la période estivale) à la baisse, le risque de sécheresse devrait considérablement augmenter d’ici la fin du siècle.
Bibliographie
Amiot L., Dubreuil V., Bonnardot V., 2023. Le changement climatique en Bretagne : cartographie sur la période observée (1951-2020) et future (2031-2100), Norois, 266, pp. 7-25.
Arnaud M., Emery X., 2000. Estimation et interpolation spatiale : méthodes déterministes et méthodes géostatistiques, Hermès science publications, Paris, 221 p.
Beauvais F., 2021. Approches géographiques et agro-climatologiques des conséquences du changement climatique sur l’agrosystème céréalier de Normandie : constat et étude d’impact prospective appliqués au blé tendre d’hiver, Géographie, Université de Caen Normandie.
Berthoumieu J-F., Debert P., Mathieu V., Legave J-M., 2022. Les conséquences des changements phénologiques sur la complémentarité et la régularité des productions fruitières, dans Legave J-M. (dir.), Les productions fruitières à l’heure du changement climatique, Versaille, Ed. Quae, pp. 193-226.
Bonnefoy C., Madelin M., Quenol H., 2014. Modélisation spatiale des températures dans le vignoble des coteaux du Layon, Revue internationale de géomatique, vol. 24, fasc. 3., pp. 377-400.
Caloz R., Collet C., 2011. Analyse spatiale de l’information géographique. Science & ingénierie de l’environnement, Lausanne, Presses polytechniques et universitaires romandes, 383 p.
Carrega P., 2003, Le climat aux échelles fines, dans Blazejczyk K., Adamczyk (dir.), XVe colloque international de l’AIC, Varsovie, pp. 19-30.
Comité 21 Grand Ouest, 2022. GIEC des Pays de la Loire - 1er rapport. 109 p.
Douguedroit A., De Saintignon M-F., 1970. Méthode d’étude de la décroissance des températures en montagne de latitude moyenne : exemple des Alpes françaises du Sud, Revue de géographie alpine, vol 58, fasc. 3, pp. 453‑472.
dubreuil v., montgobert m., planchon o., 2002. Une méthode d’interpolation des températures de l’air en Bretagne : combinaison des paramètres géographiques et des mesures infrarouge NOAA-AVHRR, Hommes et Terres du Nord, fasc. 1, pp. 26-39.
Dubreuil V., 2022. Le changement climatique en France illustré par la classification de Köppen, La Météorologie, fasc. 116, pp. 37-47.
Fortin G., Dubreuil V., 2020. A geostatistical approach to create a new climate types map at regional scale : case study of New Brunswick, Canada, Theoretical and Applied Climatology, vol. 139, fasc. 1–2, pp. 323-334.
IPCC, 2013. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, 1 535 p.
IPCC, 2021. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climat Change, Cambridge University Press, 3 949 p.
Joly D., Brossard T., Cardot H., Cavailes J., Hilal M., Wavresky P., 2008. Interpolation par recherche d’information locale. Climatologie, vol. 5, pp. 27‑47.
Joly D., Brossard T., Cardot H., Cavailes J., Hilal M., Wavresky P., 2010. Les types de climat en France, une construction spatiale, Cybergeo, vol. 501.
Jouzel J., Ouzeau G., Deque M., Jouini M., Planton S., Vautard S., 2014. Le climat de la France au XXIe siècle. Volume 4 scénarios régionalisés : édition 2014 pour la métropole et les régions d'outre-mer, Direction générale de l'Energie et du Climat, 62 p.
Koppen W., Versuch einer Klassifikation der Klimate, vorzugweise nach ihren Beziehungen zur Pflanzenwelt, Geogr. Zeitschrift, vol. 6, pp. 657-679.
Lamy C., 2013. Impact du changement climatique sur la fréquence et l’intensité des sécheresses en Bretagne, Thèse de Géographie, Université Rennes 2.
Lhotellier R., 2006. Systèmes d’information géographique et traitement de données climatiques : l’exemple de l’interpolation des températures, Analele Ştiinţifice ale Universităţii, fasc. 12, pp. 66-76.
Marano F., Toussaint J-F. , 2015, Climat et Santé, ADSP, n°93, 52p.
Merot P., Dubreuil V., Delahaye D., Desnos P. 2012. Changement climatique dans l’Ouest : évaluation, impacts, perception. Espace et territoires, Presses universitaires de Rennes, 464 p.
METEO France, 2013. Atlas climatique des Pays de la Loire, 110p.
Moisselin J-M., Scheider M., Canellas C., Mestre O., 2002. Les changements climatiques en France au XXe siècle : Etude des longues séries homogénéisées de données de température et précipitations, La météorologie, fasc. 38, pp. 45-56.
Moss R. H., Edmonds J. A., Hibbards K. A., Manning M. R., Rose S. K., Van Vuuren D. P., Carter T. R., Emori S., Kainuma M., Kram T., Meehl G. A., Mitchell J. F. B., Nakicenovic N., Riahi K., Smith S. J., Touffer R. J., Thomson A. M., Weyant J. P., Wilbanks T. J. 2010., The next generation of scenarios for climate change research and assessment’, Nature, vol. 463, pp. 747-756.
OMM, 2013. Guide des pratiques climatologiques, n°100.
Peguy P., Mounier J., Douguedroit A., 1984. Cartographie et modélisation des éléments du climat en France, Annales de géographie, vol. 516, pp. 204–217.
Ribes A., Boe J., Qasmi S., Dubuisson B., Douville H., Terray L., 2022. An updated assessment of past and future warming over France based on a regional observational constraint, Earth System Dynamic, vol. 13, pp. 1 397-1 415.
Siu-Ngang Lam N., 1983. Spatial interpolation methods: a review, The American Cartographer, vol. 10, fasc.2, pp. 129-149.
Soubeyroux J.-M., Bernus S., Corre L., Gouget V., Kerdoncuff M., Somot S., Tocquer F., 2020. Les nouvelles projections de référence Drias 2020 pour la métropole, rapport Météo France, 98 p.
Soubeyroux J.m., Martin E., Franchisteguy L., Habets F., Noilhan J., Baillon M., Regimbeau F., Vidal J-P., Le Moigne P., Morel S., 2008. Safran-Isba-Modcou (SIM) : Un outil pour le suivi hydrométéorologique opérationnel et les études, La Météorologie, vol. 63, pp. 40-45.